Треугольник

Египетский треугольник в строительстве. Общие сведения

Зарождение идеи

Надо заметить, что более двух с половиной тысяч лет назад пирамиды были несколько другими – огромными, с четкими гранями. Тщательно изучив могущественные постройки, коих было не мало, так как рядом с великанами, стояли храмы поменьше, построенные для детей, жен и других родственных лиц фараона, это натолкнуло его на мысль.

Благодаря своим математическим способностям, Пифагор сумел определить закономерность в формах пирамиды, а умение анализировать и делать выводы привели к созданию одной из самых значимых теорий в истории геометрии.

Из истории

Знали ли в древнем Египте о геометрии и математике? Конечно да. Жизнь египтян была тесно связана с наукой. Они регулярно пользовались знаниями при разметке полей, создании архитектурных шедевров. Даже существовала своя служба землемеров, которые применяли геометрические правила, занимаясь восстановлением границ.

Название треугольник получил благодаря эллинам, которые нередко бывали в Египте в VII-V вв. до н.э. Считается, что прообразом фигуры стала пирамида Хеопса, отличающаяся совершенными пропорциями. Ее место особенное в истории. Если посмотреть поперечное сечение, то можно отметить два треугольника, у которых угол внутри равняется 51о50’.

Строение

Сегодня это строение усеченной формы, приобретенной под воздействием времени, высота явно потерялась. Однако, восстановив ее геометричность, можно сделать вывод, что стороны треугольников равны. Получается в основе заложен золотой прямоугольный треугольник.

Однако, следует рассмотреть другую пирамиду – Хефрена, у которой основа как раз-таки прямоугольный треугольник и где угол наклона боковых граней равен 53о12 с соотношением катетов 4:3. Это уже так называемый священный треугольник. Для египтян такая фигура сопоставлялась с семейным очагом: катет вертикального положения олицетворял мужчину, основание – представительницу прекрасного пола, а гипотенуза – рождение ребенка от обоих.

Стороны пирамиды Хефрена в соотношении равны 3:4:5, что точно соответствует теореме Пифагора. Значит, можно сделать вывод, что строители уже знали об этой теореме, но не могли ее сформулировать. Хотя, в исторических письменах встречаются следы использования египетского треугольника за много веков даже до Египта. До сегодняшнего дня это загадка, как могли такие знания получить древние египтяне. Понимали ли они чем обладают?

Особенность фигуры к тому же в том, что благодаря подобному соотношению, она является простым и первым Героновым треугольником, так как ее стороны и площадь целочисленные.

Обратное доказательство

Таким образом теорема Пифагора стала каноном и фундаментом развития математической науки. Со школьной скамьи каждый ученик знает, что означает выражение «Пифагоровы штаны во все стороны равны».

Интересно, что теорема Пифагора находится в Книге Гиннесса как теорема, обладающая самым большим количеством доказательств, которых примерно 500.

Особенности

Если рассмотреть более детально отличительные особенности египетского треугольника, то можно выделить следующие моменты:

• все стороны и площадь состоят из целых чисел, как говорилось выше;
• согласно теории великого математика, сумма квадратов катетов равна квадрату гипотенузе;
• такой фигурой возможно отмерить прямые углы в пространстве. Это используется в процессе строительства до сих пор;
• не обязательно пользоваться специальными измерительными приборами, подойдут подручные средства, например, веревка.

Другие размеры стен и применение к ним правила «египетского треугольника»

На самом деле, если разобраться с тем, как «работает» «египетский треугольник», можно вывести стены различной длины. Главное – это их соотношение друг с другом. Попробуем разобрать этот момент на примере.

Требуется, чтобы одна из стен была равна восьми метрам. Для того чтобы соотношение получилось верным, вторую стену нужно сделать длиной 6 м. В этом случае число 8 можно обозначить как 4 отрезка по 2 м, а 6 – как 3 отрезка по 2 м. Разобравшись с длиной стен, можно свободно вывести и длину диагонали, которая будет равна квадратному корню из 6×6+8×8 (квадратный корень из 100). Получается, диагональ должна быть равна 10 м. Всё крайне просто.

ФОТО: warfields.ruМожно использовать любые размеры, главное, чтобы они имели правильное соотношение

Созвездие Треугольника

Точное происхождение названия этого созвездия неизвестно. Свое название оно получило на Древнем Востоке, его знали и использовали в навигации финикийские мореходы. Для них оно символизировало священный камень пирамидальной формы. Треугольник входил в число 48 классических созвездий античности. Древние греки считали, что это — перенесенная на небо дельта Нила, что указывает на египетские корни названия созвездия. Уже в Новое время на звездном небе были выделены созвездия Южного Треугольника и Наугольника.

Созвездие Треугольника. Иллюстрация из астрономического атласа «Уранография» Я. Гевелия

Общая формула

S = 0,5 * a * b⋅sin(α) , где a, b — стороны, α — угол между ними.

S = 0,5 * a * h, где a — основание, h — высота.

S = (a * b * c) : (4 * R), где a, b, c — стороны, R — радиус описанной окружности.

4. Площадь треугольника через вписанную окружность и стороны.

S = r * (a + b + c) : 2, где a, b, c — стороны, r — радиус вписанной окружности.

Если учитывать, что (a + b + c) : 2 — это способ поиска полупериметра. Тогда формулу можно записать следующим образом:

S = r * p, где p — полупериметр.

S = a2 : 2 * (sin(α)⋅sin(β)) : sin(180 — (α + β)), где a — сторона, α и β — прилежащие углы, γ — противолежащий угол.

6. Формула Герона для вычисления площади треугольника.

Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.

S = √ p * (p − a) * (p − b) * (p − c)​, где a, b, c — стороны, p — полупериметр, который можно найти по формуле: p = (a + b + c) : 2

Вершины углы и стороны треугольника

Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°:

+ + = 180°

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

если > , тогда >

если = , тогда =

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

+ > + > + >

Стороны треугольника пропорциональны синусам противолежащих углов.

	=		=		= 2R

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

2 = 2 + 2 — 2·

2 = 2 + 2 — 2·

2 = 2 + 2 — 2·

Площадь равнобедренного треугольника по основанию и углу между боковыми сторонами и основанием

Определение понятия

Треугольником называют фигуру, состоящую из трех соединенных между собой точек. В зависимости от углов треугольник может быть:

• Прямоугольным, если один из углов равен 90 градусов;
• Тупоугольный, если один из углов тупой, т.е. больше 90 градусов;
• Остроугольным, если все углы треугольника острые.

Для решения задач с остроугольными треугольниками часто приходится использовать теорему синусов или косинусов.

Еще в Древней Греции математики изучали треугольники. Именно греки разработали основы современной геометрии, куда входит и множество теорем о треугольниках. Например, автор теоремы Пифагора родом из Древней Греции.

Признаки равенства прямоугольных треугольников:

Признаки равенства прямоугольных треугольников основаны и вытекают из общих признаков равенства треугольников.

1. Равенство по двум катетам.

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.

Рис. 2. Равенство прямоугольных треугольников по двум катетам

АВ = А₁В₁, АС = А₁С₁

2. Равенство по катету и прилежащему острому углу.

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.

Рис. 3. Равенство прямоугольных треугольников по катету и прилежащему углу

АВ = А₁В₁, ∠АВС = ∠А₁В₁С₁

3. Равенство по гипотенузе и острому углу.

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Рис. 4. Равенство прямоугольных треугольников по гипотенузе и острому углу

ВС = В₁С₁, ∠АВС = ∠А₁В₁С₁

4. Равенство по гипотенузе и катету.

Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

Рис. 5. Равенство прямоугольных треугольников по гипотенузе и катету

ВС = В₁С₁, АС = А₁С₁ 

5. Равенство по катету и противолежащему острому углу.

Если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Рис. 6. Равенство прямоугольных треугольников по катету и противолежащему острому углу

АС = А₁С₁, ∠АВС = ∠А₁В₁С₁

О чем расскажут холмы?

Если вы решили пойти работать в военную сферу, посмотрите, есть ли у вас на холме Марса вышеуказанная геометрическая фигура. Это поможет добиться успехов и дарит расчётливость.

Бугор Венеры

Присутствие на холме Венеры – предвестник несчастий, связанных с огнём. В другой интерпретации подобный знак указывает на расчётливость в любовной сфере и семейных отношениях.

На Венере

Аполлон

Инженерами и архитекторами часто становятся обладатели треугольника на холме под безымянным пальцем, что является символом способностей в точных науках.

На Аполлоне

Сатурн

Многоугольник с тремя сторонами на холме Сатурна может выступать знаком способностей в чёрной магии, оккультизме или гипнозе. Всё таинственное и необычное может стать серьёзным занятием.

На Сатурне

Юпитер

Особый символ под указательным пальцем выдаст человека, имеющего способности красноречиво говорить.

На Юпитере

Представители знака часто становятся бизнесменами или директорами, так как всегда имеют множество идей для воплощения в реальность.

Малый треугольник

Геометрические фигуры могут иметь разную форму, ответвления и размеры. Если большой треугольник в хиромантии сулит богатство, интуицию, острый ум и гармонию в жизни, то маленький треугольник указывает на творческого человека, что обычно проявляется в раннем детстве.

Малый треугольник на ладони

Если треугольник состоит из линий Головы, Аполлона и Меркурия, то обладатель такого знака отличается особыми интеллектуальными способностями. Такой человек способен не только придумывать идеи, но и воплощать их в жизнь.

Есть знак, наделяющий обладателя философскими качествами – Ведьмин Треугольник. Символ довольно сложно найти и увидеть: одна сторона треугольника – линия Судьбы, вторая начинается на холме Сатурна, а третья – идёт от холма Меркурия.

Элементы тупоугольного треугольника:

Кроме сторон и углов у тупоугольного треугольника также имеются внешние углы. Внешний угол это угол, смежный с внутренним углом треугольника. У любого треугольника, в т.ч. тупоугольного, 6 внешних углов, по 2 на каждый внутренний. Внешний угол тупого угла тупоугольного треугольника всегда будет острым углом. Внешний угол острого угла тупоугольного треугольника всегда будет тупым углом.

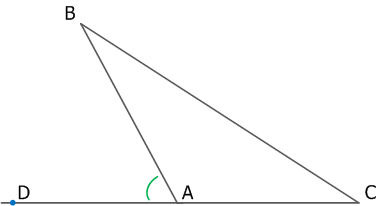
Рис. 5. Тупоугольный треугольник и внешний угол

∠ ВAD – острый угол

Медиана тупоугольного треугольника (как и любого другого треугольника), соединяющая вершину треугольника с противоположной стороной, делит ее пополам, т.е. на два одинаковых отрезка.

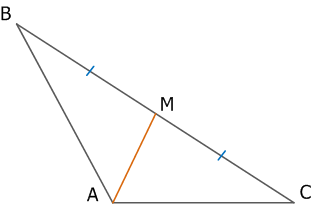
Рис. 6. Тупоугольный треугольник и медиана тупоугольного треугольника

MA – медиана тупоугольного треугольника

Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.

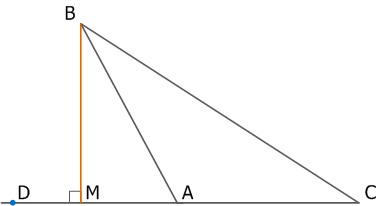
Рис. 7. Тупоугольный треугольник и высота тупоугольного треугольника

MС – высота тупоугольного треугольника

Высота тупоугольного треугольника может лежать за пределами треугольника.

Биссектриса в тупоугольном треугольнике (как и в любом другом треугольнике) делит угол пополам. Биссектрисы  пересекаются в точке, которая является центром вписанной окружности.

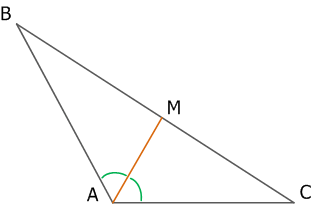
Рис. 8. Тупоугольный треугольник и биссектриса угла тупоугольного треугольника

MA – биссектриса тупого угла тупоугольного треугольника

Кроме того, биссектриса тупоугольного треугольника (как и любого другого треугольника) делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Прямоугольный треугольник

В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла. 

Некоторые свойства прямоугольного треугольника:

1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.
3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.
5. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$. (Рис.14)
6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями которых являются катеты данного треугольника. (Рис.14)

Один острый угол прямоугольного треугольника на $44°$ больше другого острого угла. Найдите больший острый угол.

Решение:

В прямоугольном треугольнике $АВС$ $∠А$ и $∠В$ – острые.

Пусть $∠ А – х$, тогда $∠ В — (х+44)$.

Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.

На основании этого правила, составим и решим уравнение:

$х+х+44=90$

$2х+44=90$

$2х=90-44$

$2х=46$

$х=23$

Угол $В$ больший в этом треугольнике, через $«х»$ он записывался как, $х+44$, следовательно, $∠В=23+44=67°$.

Ответ: $67$

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. 

$АС^2+ВС^2=АВ^2$

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$ 

Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
5. Основное тригонометрическое тождество: $sin^2x+cos^2x=1$
6. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
7. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
8. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	${1}/{2}$	${√2}/{2}$	${√3}/{2}$
$cosα$	${√3}/{2}$	${√2}/{2}$	${1}/{2}$
$tgα$	${√3}/{3}$	$1$	$√3$
$ctgα$	$√3$	$1$	${√3}/{3}$

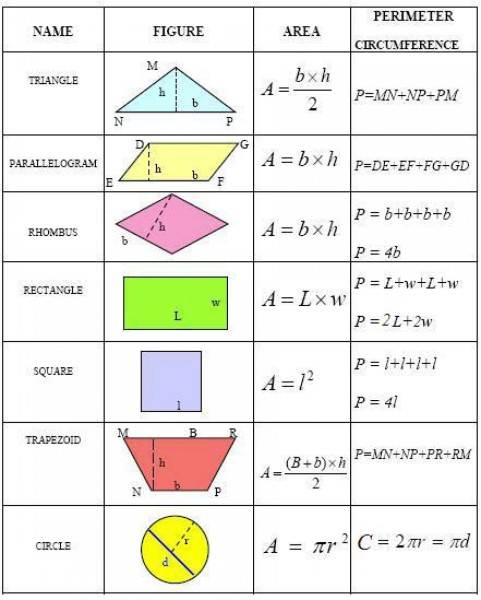
Названия геометрических фигур в картинках (23 ФОТО)

Геометрия как наука началась с древних греков. Они подстмотрели у египтян землемерные работы и оформили это в виде аксиом и правил. Первым научным трудом в этой области был «Начала» Евклида.

Объёмные геометрические фигуры

Разноцветные фигуры

Названия объёмных фигур на английском

Синие фигуры с английскими названиями

Синие фигуры с русскими названиями

Разноцветные фигуры с английскими названиями

Простые фигуры кубической сингонии

Куб, икосаэдр, тетраэдр, октаэдр, додекаэдр

Весёлые геометрические фигуры

Shapes

Конус

Треугольник, пятиугольник, шестиугольник, семиугольник, восьмиугольник

Ромб

Призмы

Пирамиды

Основные понятия относительно треугольника на ладони

Кто-то считает, что хиромантия – это категория знаний и умений, а другие склонны верить, что подобные практики – грех. Православная церковь категорически против всего, что связано с чёрной магией, узнаванием своей судьбы и различными языческими занятиями.

Треугольник на руке на линиях и его значение

Стоит знать, что треугольник может располагаться на правой и левой руке, а также на их линиях. Важную роль играют соприкосновения с линиями или нахождение на одном из холмов:

1. Под большим пальцем.
2. Под средним пальцем.
3. Безымянным пальцем.
4. Указательным пальцем.
5. Мизинцем.

Значение символа на холмах

Позитивные моменты

В хиромантии треугольники на руке, как правило, означают хорошее и светлое будущее. Такие люди часто связаны с деятельностью, требующей высокий интеллектуальных и ораторских способностей.

Положительные моменты

Чаще всего, это представители из сферы экономики, науки, политики или медицины.

Некоторые минусы

Есть и другая сторона медали: некоторые узоры сигнализируют о смерти, бедности и несчастьях. Особую роль в трактовке треугольников играет их расположение и размеры, а также сочетание с другими узорами.

В каких случаях треугольник несет негативный характер?

Как быть, если строение не подходит под размер 3×4

Понятно, что если стороны дома не подходят под заданный размер, придётся производить вычисления. Но здесь всё не так уж и сложно. К примеру, необходимо построить здание, размеры которого больше. Тогда можно сделать одну стену длиной 12 м, а вторую − 15 м. В этом случае, пользуясь всё той же теоремой Пифагора и особенностями «египетского треугольника», несложно вычислить необходимую длину диагонали (она же гипотенуза), которая будет равна 19,2 м.

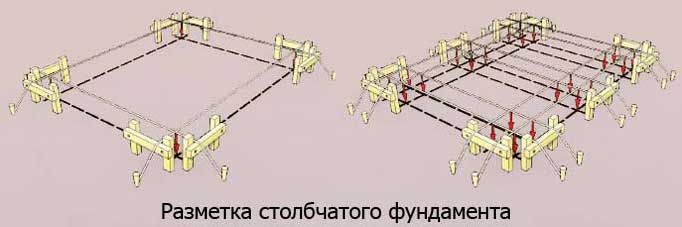
ФОТО: fsks.ruВсе углы разметки под фундамент должны быть идеально прямыми – это аксиома

«Египетский треугольник» − это способ разметки, используемый в строительстве с незапамятных времён. И то, что он и сейчас достаточно популярен, говорит о работоспособности метода. Главное – использовать его на полную, а не обходиться только поверхностными знаниями.

ФОТО: tvoidom-msk.ruЛучше потратить немного больше времени и вывести углы фундамента, чем впоследствии получить массу проблем при строительстве и отделке

Правая ладонь и треугольник

Часто рассматриваемая геометрическая фигура присутствует на одной руке или вовсе отсутствует на обеих сразу. Его значение трактуется всегда по-разному.

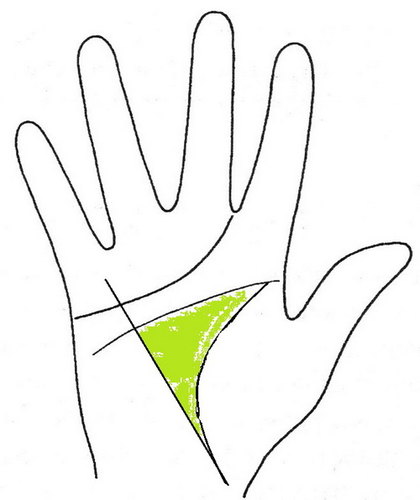Треугольник из линий

Решающую роль сыграют следующие детали:

1. Соприкосновение с линиями Головы и Судьбы сулит человеку хорошее финансовое будущее, но свои деньги придётся зарабатываться нелёгким трудом. А увеличение достатка будет зависеть от линии Ума.
2. В хиромантии большой треугольник на ладони сулит денежный успех, но важны чёткие линии.
3. Если в общей картине фигуры есть разрывы, то деньги будут легко тратиться, не задумываясь о целесообразности.

Популярные темы сообщений

• Паук Тарантул

  Если сказать простым языком, то тарантул это большой паук, который имеет ядовитые железы. Тарантул относится к классу членистоногих, но к разряду паукообразных. История тарантула и его названия не дошла до наших дней,

• Большой Кремлевский дворец

  Большой Кремлевский дворец находится в столице нашей Родины в городе Москве. Он входит в состав дворцов Московского Кремля. Строительство Дворца началось в 1838 г, по приказу Всероссийского императора Николая 1

• Ученые

  Учёные — это люди, которые внесли важный вклад в науку. Они совершают открытия и проводят исследования в различных областях науки. Таким образом, учёных можно разделить на несколько категорий: физики, химики, математики, филологи, астрономы,

Свойства остроугольного треугольника:

Свойства остроугольного треугольника аналогичны свойствам обычного треугольника:

1. Против большей стороны лежит больший угол, и наоборот.

Рис. 8. Остроугольный треугольник

2. Против равных сторон лежат равные углы, и наоборот.

Рис. 9. Остроугольный треугольник с равными боковыми сторонами

АВ = ВС

3. Сумма углов остроугольного треугольника равна 180°.

4. Любая сторона остроугольного треугольника меньше суммы двух других сторон и больше их разности:

• • a < b + c;
  • a > b – c;
  • b < a + c,
  • b > a – c;
  • c < a + b;
  • c > a – b.

Примечание:  Фото https://www.pexels.com, https://pixabay.com

карта сайта

Коэффициент востребованности
1 602

Треугольник Кеплера

В начале XVII в. знаменитый астроном Кеплер составил диаграмму соединения планет Сатурна и Юпитера. Так в астрономии называют расположение планет, при котором для земного наблюдателя эклиптические долготы равны нулю, а сами небесные тела находятся близко друг к другу или даже перекрываются. Кеплер представил это явление в виде треугольника, который вращается по зодиакальному кругу, совершая полный оборот за 2400 лет.

Великий треугольник соединения Сатурна и Юпитера

Четыре стихии: Земля, Вода, Воздух и Огонь. Миниатюра из алхимического трактата XVII в.

Рождение Сына Солнца из Философского яйца. Миниатюра из алхимического трактата XVII в.

Король Земли поклоняется философской сере. Миниатюра из алхимического трактата XVII в.

Понятие треугольника

Вспомним следующую аксиому для такого основного понятия геометрии, как прямая.

Аксиома 1: Можно найти как минимум три точки, которые не будут лежать на одной и той же прямой.

Выберем на плоскости три произвольные точки, которые будут удовлетворять условию аксиомы 1. Соединим эти точки между собой отрезками. Тогда

Определение 1

Треугольником будем называть такую геометрическую фигуру, которая состоит из трех точек, не имеющих общей прямой, соединенных отрезками.

Определение 2

Точки в рамках определения 1 называются вершинами треугольника.

Определение 3

Отрезки в рамках определения 1 называются сторонами треугольника.

Треугольник будем обозначать тремя точками его вершин (рис. 1)

Правая и левая рука

В хиромантии с древних времен передаются знания, позволяющие читать прошлое и будущее человека. Эзотерики уверены, что одни и те же знаки на разных руках несут различную информацию.

За тысячелетия существования хиромантии эзотерики заметили, что существуют определенные «стандартные» послания на правой и левой руке.

Так, ведущая рука несет знание о:

• будущем человека;
• эмоциях и душевных переживаниях человека;
• ситуациях, которые являются результатом действий и решений самого человека;
• риске возникновения какого-либо заболевания.

Например, треугольник на левой руке на линии жизни несет очень много информации о человеке

По пассивной руке узнают о:

• прошлом;
• предрасположенности к магии;
• сильных сторонах характера;
• прирожденных талантах;
• «планах» Судьбы на этого человека – событиях, которые невозможно предотвратить.

Биссектрисы треугольника

Определение. Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.

Свойства биссектрис треугольника:

1. Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, — центре вписанной окружности.

2. Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

   AEAB = ECBC

3. Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.

   Угол между и ‘ = 90°

4. Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный.

Глупая ошибка строителей

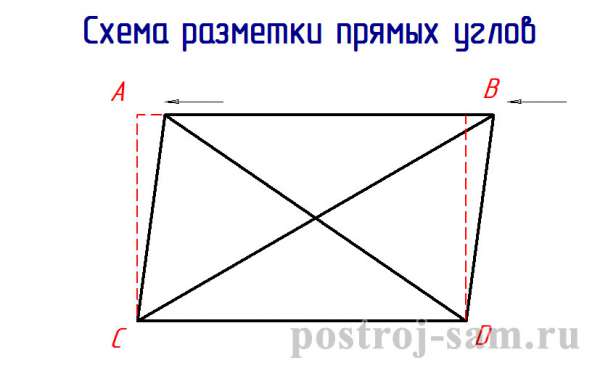
«Египетский треугольник» действительно может помочь в разметке периметра фундамента, однако применение этого метода требует сохранения чётких пропорций. Небольшое отклонение от них − и угол уже не будет прямым. А это приведёт к разнице длин стен. Не единичны случаи, когда при идеальном совпадении длин диагоналей стены получаются разными. Ведь если вдуматься, то трапеция также подходит под заданные параметры, её диагонали равны, в то время как верхняя и нижняя сторона имеют разные длины.

ФОТО: youc.irПравильная трапеция также имеет одинаковые длины диагоналей, однако на квадрат она явно не тянет

их разности ( a < b + c, a > b – c; b < a + c, b > a – c; c < a + b, c > a – b ).

Признаки равенства
треугольников.

Треугольники равны, если у них
соответственно равны:

a) 
две стороны и угол между ними;

b) 
два угла и прилегающая к ним сторона;

c) 
три стороны.

Признаки равенства прямоугольных треугольников. 

Два прямоугольных треугольника равны, если
выполняется одно из следующих условий:

1)  равны их катеты;

2)  катет и гипотенуза одного треугольника равны катету и гипотенузе другого;

3)  гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу
другого;

4)  катет и прилежащий острый угол одного треугольника равны катету и
прилежащему острому углу другого;

5)  катет и противолежащий острый угол одного треугольника равны катету и
противолежащему
острому углу другого.

Замечательные линии и точки в
треугольнике.

Высота
треугольника — этоперпендикуляр,опущенный из любой вершины
на противоположную сторону
(
или её продолжение).Эта сторона называетсяоснованием треугольника.Три высотытреугольникавсегдапересекаютсяв одной точке,
называемой ортоцентром треугольника.Ортоцентр остроугольного
треугольника ( точка O,
рис.26 ) расположен внутри треугольника, аортоцентр тупоугольного
треугольника ( точка O,
рис.27 ) – снаружи; ортоцентр прямоугольного треугольника совпадает с
вершиной прямого угла.

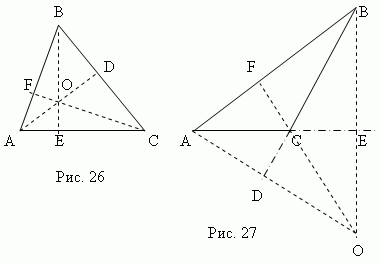
Медиана
– это отрезок,
соединяющий любую вершину треугольника с серединой противоположной стороны.Три медианы треугольника
(AD,BE,CF,
рис.28 ) пересекаются в
одной точке
O,
всегда лежащей внутри треугольникаиявляющейсяегоцентром тяжести.Эта точка делит каждую
медиану в отношении 2:1, считая от вершины.

Биссектриса
– этоотрезок биссектрисыуглаот вершины доточкипересечения с противоположной
стороной.
Три биссектрисы треугольника
( AD,
BE,
CF,
рис.29 ) пересекаются в
одной точке О, всегда
лежащей внутри треугольникаиявляющейся центром
вписанного круга (см. раздел «Вписанныеи описанные многоугольники»).

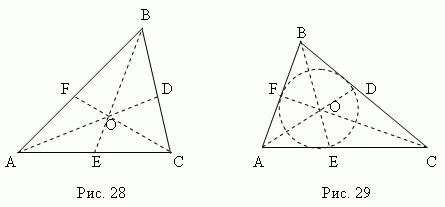
Биссектриса делит противоположную
сторону на части, пропорциональные прилегающим сторонам;
например, на  рис.29  AECE
= ABBC
.

Срединный перпендикуляр
– это перпендикуляр,
проведенный из средней
точкиотрезка(стороны).Три срединных перпендикуляра
треугольника АВС
(KO,
MO,
NO,
рис.30
) пересекаются в одной точке О,
являющейся центром

описанного круга
( точки K,
M,
N
– середины сторон треугольника
ABC
).

В остроугольном треугольнике эта точка
лежит внутри треугольника; в тупоугольном – снаружи; в прямоугольном
-в середине гипотенузы.
Ортоцентр, центр тяжести, центр описанного и
центр вписанного круга
совпадают только в равностороннем
треугольнике.

Теорема Пифагора. В
прямоугольном треугольнике квадрат длиныгипотенузы равен сумме
квадратов длин катетов.

Доказательство теоремы Пифагора с
очевидностью следует из рис.31.
Рассмотрим прямоугольный треугольник
ABCс катетамиa,
bи гипотенузой
c.

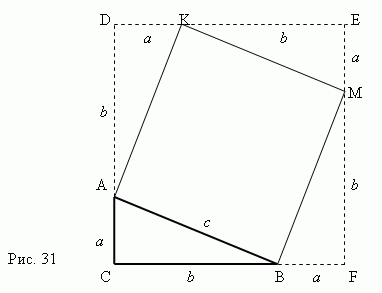
Построим квадрат
AKMB,
используя гипотенузу AB
как сторону. Затемпродолжим стороны
прямоугольного треугольника ABC
так, чтобы получить квадрат
CDEF,
сторона которого равна  a+
b
. Теперь ясно, что площадь
квадрата CDEF
равна (a+b)2.
С
другойстороны,этаплощадь равна суммеплощадейчетырёх прямоугольных
треугольников
иквадрата
AKMB,
то есть

c2
+ 4 ( ab
/ 2 ) = c2
+ 2 ab
,

отсюда, 

c2 +
2 ab =( a + b )2 ,

и окончательно имеем:

c2=  a2
+ b2.

Соотношение сторон в
произвольном треугольнике.

В общем случае ( для произвольного
треугольника ) имеем:

c2= a2
+ b2
– 2ab ·cosC,

где
C
– угол между сторонами  a 
и  b
.  

Откуда взялся символ валькнут

Валькнут, представляющий собой знак, вмещающий три треугольника, чаще всего встречается на рунических камнях, жертвенниках и изображениях битв или казней.

Также этот знак обнаруживался на ритуальных принадлежностях для погребения.

Традиционно этот символ выбивался на жертвенных камнях, предназначенных для осуществления казни «кровавый орел».

В ходе казни еще живому человеку рассекали ребра, выворачивали их в стороны и доставали легкие. Последние клали на плечи казнимому наподобие крыльев.

Такой способ казни применялся к врагам, плененным в ходе военных конфликтов, а в некоторых источниках описывается как способ мести (например, за убийство).

Это считалось принесением жертвы Одину, поэтому валькнут, как непременный атрибут такого жертвенника, и связывают с этим богом.

По значению валькнут, скорее всего, отображал некий «путь воина»: от земного существования до Вальхаллы и встречи с Одином.

Также археологи находили валькнут на оружии и доспехах. Предположительно, знак наносился также в качестве ритуальной татуировки воинам, посылаемым на смерть, то есть в бой, с которого был крайне мал шанс вернуться.

Очевидно, что таким образом воина заблаговременно готовили к загробной жизни.

Высоты треугольника

Определение. Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.

В зависимости от типа треугольника высота может содержаться

• внутри треугольника — для остроугольного треугольника;
• совпадать с его стороной — для катета прямоугольного треугольника;
• проходить вне треугольника — для острых углов тупоугольного треугольника.

Свойства высот треугольника

Высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.
Если в треугольнике две высоты равны, то треугольник — равнобедренный.

:: = 1:1:1 = ():():()

1 + 1 + 1 = 1

Числовой символизм валькнута

Числа играют очень важную роль во всех языческих религиях. Числовой символизм, соответственно, присущ и скандинавскому язычеству.

Числа, отраженные в изображении «узла павших» — это 3 и 9. Они имеют свое собственные сакральное значение. 9 – это число миров в скандинавской мифологии:

1. Мир богов или Асгард.
2. Мир людей или Мидгард.
3. Мир умерших или Хельхейм.
4. Мир ванов или Ванахейм.
5. Мир великанов или Йотунхейм.
6. Мир светлых альвов или Альвхейм.
7. Мир огненных великанов или Муспельхейм.
8. Мир ледяных великанов или Нифльхейм.
9. Мир карликов или Свартальфахейм.

Также 9 – число ветвей мирового ясеня Иггдрассиля (по одному
на каждый мир). 9 ветвей – основа рун старшего алфавита (футарка). 3 – число
норн (богинь судьбы), отражающее настоящее, прошлое и будущее.

Иные способы выведения прямого угла

Если нет желания заниматься выведением углов самостоятельно, а финансы позволяют обратиться за помощью к специалистам, можно вообще не думать об этом вопросе. Один звонок − и на участке уже находится геодезист с теоделитом, который в сжатые сроки сделает разметку. Однако в этом случае необходимо быть готовым к внушительным затратам на оплату его труда.

ФОТО: omegagalvanoplastia.com.brТеоделит – высокоточная техника, однако стоимость подобной разметки может влететь «в копеечку»

Если говорить о минимальных затратах, то, основываясь на прайс-листах фирм, оказывающих подобные услуги, вызов и работа геодезиста с инструментом обойдётся в 1 000 руб./час при минимальной оплате 7 000 руб. Дальше − больше. Разметка осей (2 точки) – ещё 3 000 рублей. Если же потребуется определить точные координаты по GPS, то здесь каждые три точки обойдутся владельцу в 5 000 руб. Можно посчитать, какова будет общая сумма (все цены указаны с учётом на конец сентября 2020 года). Не проще ли самому произвести все необходимые разметки? Ведь сэкономленные средства всегда можно потратить на что-то полезное в дальнейшем строительстве.

ФОТО: thelundreport.orgСтоит приготовиться к тому, что карман значительно облегчится

Равносторонний треугольник (понятие, определение):

Равносторонний треугольник – это треугольник, у которого все стороны равны между собой по длине, все углы также равны и составляют 60°.

Равносторонний треугольник называется также правильным или равноугольным треугольником.

По определению, каждый правильный (равносторонний) треугольник также является равнобедренным, но не каждый равнобедренный треугольник – правильным (равносторонним). Иными словами, правильный (равносторонний) треугольник является частным случаем равнобедренного треугольника.

Рис. 1. Равносторонний треугольник

АВ = ВС = АС – стороны треугольника, ∠ АВС = ∠ BАC = ∠ BСA = 60° – углы треугольника

Небольшие хитрости

Египетский треугольник 3х4х5 актуален для маленьких домов. Но, что делать, если дом 12х15?

Для этого нужно построить прямоугольный треугольник, у которого катеты равняются 12 и 15 м. Гипотенуза находится как квадратный корень из суммы 12х12 и 15х15. В итоге получаем 19,2 м. С помощью чего-либо — веревки, шпагата, бечевки, тросика, военного кабеля, отмеряем 12, 15 и 19,2 м. Делаем узлы на этих местах и ставим жимки.

Затем треугольник нужно растянуть на нужном месте и установить 3 точки опоры, в которые вбить колышки. Четвертую точку можно получить, не трогая концы катетов. Для этого точка прямого угла перекидывается по диагонали и все готово.

Например, есть участок, где требуется прямой угол – для места под кухонный гарнитур, раскладки кафеля и других моментов. Хорошо бы такие вопросы учесть при кладке, но реальность другая и не всегда попадаются ровные стены и прямые углы. Здесь пригодится египетский треугольник с соотношением 3:4:5, либо при необходимости 1,5:2:2,5.

Обязательно учитывается толщина маяков, погрешность, бугры на стенах и т.д. Треугольник рисуется с помощью рулетки и мела. Если разметка небольшая, то можно воспользоваться листом гипсокартона, так как режутся они с правильными углами.

Египетский треугольник широко использовался в строительстве целых 2,5 века. И сегодня иногда приходится применять данную методику, при отсутствии необходимых инструментов, чтобы получить прямые углы. Свойства этой фигуры уникальны, что гарантирует точность в архитектуре и строительстве, без которой не обойтись. С ним легко работать, по форме он гармоничен и красив. До сих пор пытливые умы пытаются разгадать тайну египетского треугольника.

[править] Основные факты

Вершины треугольника обычно обозначают большими латинскими буквами A, B, C, углы при соответствующих вершинах греческими буквами α, β, γ, а длины противоположных сторон — маленькими латинскими буквами a, b, c.

Сумма внутренних углов треугольника — 180 градусов. Внешний угол треугольника (угол смежный к внутреннему углу) всегда равен сумме двух других внутренних углов треугольника. Как и у всех выпуклых многогранниках сумма внешних углов треугольника 360 градусов.

\alpha+ \beta+ \gamma\ = 180^\circ

Сумма длин двух любых сторон треугольника всегда превышает длину третьей стороны. Это неравенство треугольника или аксиома треугольника (в частном случае равенства два угла уменьшаются до нуля и треугольник вырождается в отрезок).